Matrix multiplication (Version 2) - Tiled Matmul

Building on our naive matrix multiplication implementation, we’ll now explore tiled matrix multiplication - a crucial optimization technique that dramatically improves performance by leveraging the GPU’s memory hierarchy. This approach addresses the memory bandwidth limitations we discussed in our CUDA memory model post.

Why Tiling Matters

The naive approach suffers from poor compute-to-memory access ratio (arithmetic intensity). Each element is loaded multiple times from global memory, making the kernel memory-bound. Tiling solves this by reusing data in fast on-chip memories.

The Problem with Naive Matrix Multiplication

Our previous naive implementation has a fundamental limitation: each element of matrices A and B is loaded from global memory multiple times. For a matrix multiplication C = A × B:

• Each element of A is loaded n times (once for each column of B)
• Each element of B is loaded m times (once for each row of A)
• This results in very low arithmetic intensity: 0.25 FLOP/B

The Tiling Strategy

Tiling divides the computation into smaller tiles that fit in fast on-chip memory (shared memory). The key insight is:

1. Load tiles of A and B into shared memory
2. Compute partial results using the tiles
3. Reuse the loaded data for multiple computations
4. Accumulate results in registers

Mathematical Foundation

For matrices A (M×K), B (K×N), and C (M×N), we partition them into tiles:

• A is divided into tiles of size TILE_SIZE × TILE_SIZE
• B is divided into tiles of size TILE_SIZE × TILE_SIZE
• C is computed tile by tile

Each tile of C is computed as: $C_{tile}={\sum }_{k=0}^{K/TILE\_SIZE}{A}_{tile,k}\times B_{tile,k}$

CUDA Implementation

Kernel Design

__global__ void tiledMatMul(float* A, float* B, float* C, int M, int N, int K) {
    // Allowcate Shared memory for tiles
    
    
    // Iterate over tiles
    for (int tile = 0; tile < (K + TILE_SIZE - 1) / TILE_SIZE; tile++) {
        // Load tile of A into shared memory
        
        // Load tile of B into shared memory
        
        // Synchronize to ensure all threads have loaded their data
        __syncthreads();
        
        // Compute partial result using shared memory
        }
        
        // Synchronize before loading next tile
        __syncthreads();
    }
    
    // Write result to global memory
}

Thread Block Configuration

// Launch configuration
dim3 blockSize(TILE_SIZE, TILE_SIZE);  // 16x16 = 256 threads per block
dim3 gridSize((N + TILE_SIZE - 1) / TILE_SIZE, 
              (M + TILE_SIZE - 1) / TILE_SIZE);
 
tiledMatMul<<<gridSize, blockSize>>>(A, B, C, M, N, K);

Handling Out-of-Bounds Matrix Access

When matrices don’t divide evenly by the tile size, we need to handle boundary conditions carefully. Let’s examine a concrete example:

Out-of-Bounds Example

Matrix dimensions: A(1000×800), B(800×1200), C(1000×1200) Tile size: 16×16

Grid configuration:

• Grid X: (1200 + 16 - 1) / 16 = 75 blocks
• Grid Y: (1000 + 16 - 1) / 16 = 63 blocks
• Total: 75 × 63 = 4,725 blocks

Boundary cases:

• Rightmost tiles: Columns 1184-1199 (partial tile)
• Bottom tiles: Rows 992-999 (partial tile)
• Last tile in K dimension: K=800, tile covers 784-799

Boundary Condition Analysis

// Example: Thread at (tx=8, ty=12) in block (bx=74, by=62)
int row = by * TILE_SIZE + ty;  // 62*16 + 12 = 1004
int col = bx * TILE_SIZE + tx;  // 74*16 + 8 = 1192
 
// For matrix A (1000×800):
if (row < M && (tile * TILE_SIZE + tx) < K) {
    // row = 1004 >= 1000 → FALSE, so As[ty][tx] = 0.0f
    As[ty][tx] = A[row * K + tile * TILE_SIZE + tx];
} else {
    As[ty][tx] = 0.0f;  // ← This executes
}
 
// For matrix B (800×1200):
if ((tile * TILE_SIZE + ty) < K && col < N) {
    // col = 1192 < 1200 → TRUE, but depends on tile
    Bs[ty][tx] = B[(tile * TILE_SIZE + ty) * N + col];
} else {
    Bs[ty][tx] = 0.0f;  // ← May execute for last tile
}

Why Zero Padding Works

Zero Padding Strategy

Setting out-of-bounds elements to 0.0f is safe because:

• Multiplication by zero: 0 × anything = 0
• Addition of zero: sum + 0 = sum (no effect)
• Preserves correctness: Final result is unchanged

Alternative approaches:

• Skip computation for out-of-bounds threads
• Use separate kernels for boundary tiles
• Pad matrices to tile-aligned dimensions

Complete Kernel With Boundary Handling

__global__ void tiledMatMulSafe(float* A, float* B, float* C, int M, int N, int K) {
    __shared__ float As[TILE_SIZE][TILE_SIZE];
    __shared__ float Bs[TILE_SIZE][TILE_SIZE];
    
    int tx = threadIdx.x;
    int ty = threadIdx.y;
    int bx = blockIdx.x;
    int by = blockIdx.y;
    
    int row = by * TILE_SIZE + ty;
    int col = bx * TILE_SIZE + tx;
    
    float sum = 0.0f;
    
    for (int tile = 0; tile < (K + TILE_SIZE - 1) / TILE_SIZE; tile++) {
        // Load A tile with bounds checking
        int A_col = tile * TILE_SIZE + tx;
        if (row < M && A_col < K) {
            As[ty][tx] = A[row * K + A_col];
        } else {
            As[ty][tx] = 0.0f;
        }
        
        // Load B tile with bounds checking  
        int B_row = tile * TILE_SIZE + ty;
        if (B_row < K && col < N) {
            Bs[ty][tx] = B[B_row * N + col];
        } else {
            Bs[ty][tx] = 0.0f;
        }
        
        __syncthreads();
        
        // Compute with bounds checking
        for (int k = 0; k < TILE_SIZE; k++) {
            int A_k = tile * TILE_SIZE + k;
            if (A_k < K) {  // Only multiply if within bounds
                sum += As[ty][k] * Bs[k][tx];
            }
        }
        
        __syncthreads();
    }
    
    // Write result with bounds checking
    if (row < M && col < N) {
        C[row * N + col] = sum;
    }
}

Memory Hierarchy Utilization

Memory Usage Breakdown

• Global memory: Initial tile loads (coalesced access)
• Shared memory: Tile storage and reuse (fast on-chip access)
• Registers: Accumulation variable sum (fastest access)
• Constant memory: Could store TILE_SIZE if needed

Comparison with Naive Implementation

Let assume that, we use kernel with tile size $T\times T$ and $M,N,K$ can be divided by $T$

Aspect	Naive	Tiled
Shared Memory	Not used	$T\times T$
Performance	Memory-bound	Near compute-bound
Code Complexity	Simple	Moderate
Arithmetic Intensity	0.25 FLOP/B	16+ FLOP/B
Memory Traffic	$2\times M\times N\times K$	$(M\times K)\times (N/T)+(K\times N)\times (M/T)$

In general compare to naive implementation the memory traffic is reduced by a factor of $T$ and branch divergence affects only blocks on boundaries, and should be small for large matrices.

Memory Access Analysis

Assume that the following matrix size specifications are passed to your tiled matrix multiplication kernel in MP3: numARows=55 numAColumns=48 numBRows=48 numBColumns=43 numCRows=55 numCColumns=43 Remember that the matrices contain floats.

Also assume that you are using $16\times 16$ tiles.

How many Bytes are read from global memory by the kernel?

Answer: 64704

How many Bytes are written to global memory by the kernel?

Answer: 9460

Tiled Matrix Multiplication Computation Use

Assume that the following matrix size specifications are passed to your tiled matrix multiplication kernel in MP3: numARows=142 numAColumns=110 numBRows=110 numBColumns=146 numCRows=142 numCColumns=146 Remember that the matrices contain floats.

Also assume that you are using $32\times 32$ tiles.

Recall that floating-point arithmetic operations include mathematical operations such as addition and multiplication.

Consider a matrix multiplication implementation where only threads responsible for an element in the output matrix C are required to perform floating-point operations. How many floating-point operations are executed in this implementation with respect to the parameters above?

solution: 4561040

Now consider an implementation where all threads launched perform floating-point operations. How many floating-point operations are executed now?

solution: 6553600

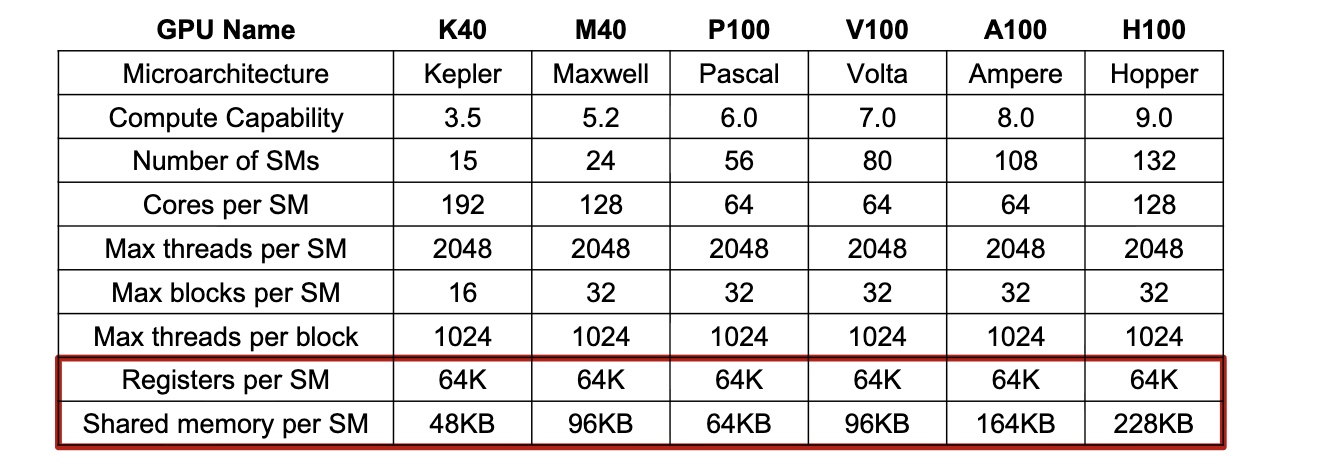
Hardware Constraints to Consider

• Registers per SM: 64K(32-bit registers)
• Shared Memory per SM: 48KB-164KB
• Threads per SM: 1024-2048 concurrent threads

Register usage per thread, and shared memory usage per thread block constrain occupancy

Tile Size	Shared Memory	Use Case
32×32	8KB	Conservative, works on most GPUs
64×64	32KB	High-end GPUs, good performance
128×128	128KB	Modern GPUs with large shared memory

Selection Strategy

1. Start conservative with 32×32
2. Profile different sizes on target hardware
3. Check occupancy (aim for >50%)
4. Monitor for register spilling
5. Measure actual performance

Quick Decision Tree

• If (GPU is modern Volta/Ampere) → Try 64×64 or 128×128
• Else if (GPU is Pascal or older) → Use 32×32
• Always Validate with profiling

I will try to cover ways to calculate tile size for maximum occupancy in a future blog post.

Key Takeaway

Empirical testing beats theoretical calculation - compiler optimizations and memory patterns significantly impact actual resource usage.

When to Use Tiling

Tiling is most beneficial when:

• Matrices are large enough to benefit from data reuse
• Memory bandwidth is the bottleneck (not compute)
• You have sufficient shared memory per block
• The algorithm has regular access patterns

Best Practices

Implementation Guidelines

1. Choose appropriate tile size: Balance shared memory usage vs occupancy
2. Use appropriate synchronization: __syncthreads() at the right points
3. Handle boundary conditions: Check array bounds for partial tiles

Summary

Tiled matrix multiplication demonstrates the power of understanding GPU memory hierarchy. By strategically using shared memory to reuse data, we can:

• Increase arithmetic intensity and Reduce memory traffic by a factor of $TIL{E}_{S}IZE$
• Achieve near-peak performance on modern GPUs
• Transform memory-bound kernels into compute-bound ones The key insight is that data reuse is often more valuable than raw computational power. This principle applies to many other GPU algorithms beyond matrix multiplication.

---

References

Hwu, W.-M. W., Kirk, D. B., & El Hajj, I. (2022). Programming massively parallel processors (4th ed.). doi:10.1016/c2020-0-02969-5